Game theory is a field of math that concerns optimal independent decision making by several players, when each decision affects the other players. It used to be very useful in many fields of science, eg in biology, economy, IT or social science.

A good example of game theory's existence in everyday life can be the situation, where a driver is getting close to the zebra crossing and notices a pedestrian. The possibilities for a driver are to keep constant speed, speed up, slow down or stop. Pedestrian can wait for a car to pass through or not. Participants make their decisions keeping in mind what are the other's possible strategies and choosing the best option. Other example can be a producer deciding about the quality of product regarding to the market reaction and expected profit (the cost of production vs profit from the sale of product).

Let's consider a number of players, and assume that each makes an independent decision.
Each player can choose one of the set of its own strategies – available decisions. A complete set of players with a particular decision chosen by each one is a point in a multidimensional space that contains scores for each players in this actual situation. The higher the score rate, the more favorable is this situation for a player.

A Hicks optimum is a point in a space in which the sum of scores for all players is the highest in the whole space.
A Nash equilibrium is a point in a space in which no one would change his decision, if they knew decisions of the other players before.
An attractor here is a Nash equilibrium and also an area where other points from the space would evolve towards that equilibrium (according to preference directions of players). A set of points aiming at one attractor defines its basin of attraction.

An example game theory's problem

One of common examples of applying game theory is a Prisoner's Dilemma. The intuition is here as following. Two people were caught on failed attempt of robbery. They are also suspects of a serious crime. Though, there are no proofs against them. After being separated, they both get a possibility of testifying against the other in exchange for commuting a sentence. In this problem they both have 2 strategies available (cooperation and keeping silence). After making decisions by both prisoners, they will get to know the effects (see the score matrix, Fig. 1). In case of keeping silence by both prisoners, no one will have a benefit from this situation. When both cooperate, each prisoner is incriminated, yet the punishment is slightly softened. If one prisoner cooperates and second does not, the first one's punishment is softened and the second one becomes incriminated.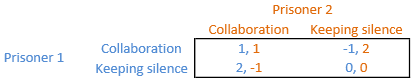


Fig. 1. An example score matrix

Such score matrix can be modeled using applet. After choosing "Insert" from the configuration menu, select 2 players and continue. An optional step is giving names for problem instance, players and their strategies. After adding 2 players the viewing panels appear. The score matrix is being visualized in 2D or 3D (regarding the number of players). Each point in the space corresponds to set of decisions made. After selecting appropriate point (by clicking the sphere or selecting coordinates from the menu) it is possible to modify scores for each player in particular situation. After setting a scores (see the score matrix, Fig. 1) one can see the game theory's features measured (choosing from "Determine features" menu). When choosing particular features, it is easy to notice, that the highest sum of benefits is when both prisoners cooperate (Hicks Optimum). However, prisoners cannot communicate and choose the best strategy regardless the other prisoner's decision - cooperation (Nash Equilibrium).

The applet

Choose the interface language:

The applet – description

Choosing configuration

The application's main menu (Fig. 2) lets the user choose a configuration in 3 different ways:

• The first button leads to the defining-new-configuration mode.
  • After clicking it, a configuration panel shows up (Fig. 3). It allows the user to change the instance name or the number of players.
    • Proceed to activate the edit-players panel (Fig. 4). Here the user can change the player name and the number and names of strategies. Finally, after adding the set of players, the space-viewing panel in edit mode appears (Fig. 6). Here one can modify the scores for players.
• The middle button allows to load one of the predefined configurations. After clicking, the panel with available instances appears (Fig. 5).
• The last button opens a window, where a file with a particular instance can be loaded.

Once the configuration is ready, a viewing panel shows up:

• in edit mode (Fig. 6) – for the new configuration
• in features mode (Fig. 7) – for the loaded configuration

Fig. 2. Main menu

Fig. 3. Configuration panel

Fig. 4. Edit-players panel

Fig. 5. Choose-configuration panel

Viewing the space

When viewing the space, there are 2 modes available: edit mode and features mode. The shared components are:

• Configuration panel with a save-to-file option,
• Control panel where the user chooses one of the modes or goes back to menu,
• Space viewer panel (in different display modes).

The edit mode

The distinctive feature of the edit mode (Fig. 6) is a panel where the user can choose an element and change its scores for all the players. The x, y and z axes represent players, and the color in the panel corresponds to the proper axis in the space viewer. Changing the strategy for one of the players is equivalent to a transition in the space. The actual position (or the set defined by choices of some players) is emphasized with a distinct color in the space viewer.

The features mode

In this mode (Fig. 7) there is a possibility to count the game theory features for a particular instance of a game. The mentioned features are Hicks optima and Nash equilibria with basins of attraction. The Hicks optima are emphasized with one distinct color. For Nash equilibria, each one found is shown with a unique color. The basins are visualized using the attraction factors and the colors of the appropriate attractors that correspond to a particular point in the space.

Fig. 6. Edit mode

Fig. 7. Features mode

Technical details: the algorithms employed

Finding the Hicks optima: for all the points in the space, the sum of scores for all players is being counted. The Hicks optimum is a point where the sum of scores is maximal.

Finding the Nash equilibria and its attraction basins is described below.

• Finding the Nash equilibria
  • Find all the points of space where for each player:
    • current player could not make a choice better than actual, if they knows decisions of other players.
• Finding the basins of attraction
  • For each point in the space:
    • If it is a Nash equilibrium, continue to the next point in space
    • Repeat for a number of times (eg. 10 000 times)
      • Starting from this point, as long as the actual position is not a Nash equlibrium, repeat:
        • Draw a player (with equal probabilities)
        • Let the chosen player change their strategy to one of these that give them the highest score (with equal probabilities, and while decisions of other players do not change)
    • Find all the attractors achievable from the initial point and count the attractiveness factors (times finished in the attractor divided by the total number of experiments)
    • Visualize the point using its achievable attractors and attractiveness factors.

Useful sources

• Game Theory – Theodore L. Turocy, Bernhard von Stengel
• http://en.wikipedia.org/wiki/Game_theory
• http://en.wikipedia.org/wiki/Attractor

Program and text: Marcin Samsonowski

Mentor: Maciej Komosinski